Problemas de matemáticas (con solución) que pondrán a prueba tu lógica

Hay problemas de matemáticos que parecen fáciles de resolver, aunque luego requieren de cálculos complejos; los hay que parecen difíciles y faltan datos, aunque posteriormente tienen una solución sencilla. Sea como fuere, las matemáticas requieren de atención, lógica y conocer unos cuantos conceptos. Y, es importante leer bien el enunciado antes de ponerse a hacer cálculos.

Te presentamos una serie de problemas de matemáticas que pondrán a prueba tu lógica, ingenio y capacidad para el cálculo. Todos ellos tienen solución que te recomendamos ver solo cuando los hayas resuelto o cuando lleves un rato pensando y seas incapaz de encontrar la solución. 

Ver también: Problemas de matemáticas para secundaria

Problemas de matemáticas para estimular la lógica y el razonamiento

 

1. Cuestión de probabilidades

Un grupo de amigos ha quedado en un restaurante a cenar. Han acudido Jesús, Bruno, Carlos y Diego con sus mujeres Alicia, Bea, Cris y Delia. Los ocho se sientan al azar alrededor de la mesa redonda que ya está dispuesta. ¿Qué probabilidades hay de que Carlos se siente al lado de su mujer?

 

Solución: este es un problema de matemáticas en el que hay que hacer un cálculo de probabilidades. Una vez que se han sentado todos, incluido Carlos, su mujer Cris, tiene 7 sillas donde poder sentarse. De estas, 2 son contiguas a la de su marido. Por lo tanto, la probabilidad de que Carlos se siente al lado de su mujer es de 2/7.

2. Tartas y niños

Un niño y medio se comen una tarta y media en un un minuto y medio. ¿Cuántos niños harán falta para comer 60 tartas en media hora?

 

Solución: si un niño y medio se comen una tarta y media en un minuto y medio, en ese mismo minuto y medio, un niño se come una tarta. Por lo tanto, un niño se come 2 tartas en 3 minutos y 20 tartas en media hora. De esta manera, si un niño come 20 tartas en media hora, se necesitan 3 niños para comer 60 tartas en media hora.

3. Silogismo matemático

Álvaro le dice a Julio: 

- Cuando digo la verdad, tú también.

Julio contesta: 

- Cuando yo miento, tú también.

¿Es posible que en esta ocasión uno mienta y el otro no?

 

Solución: digamos que la afirmación de Álvaro es A y la de Julio es B.

• Si A es falsa, habrá ocasiones en que A diga la verdad y B mienta. Por lo tanto, la afirmación de B también será falsa.
• Si la afirmación de B es falsa, habrá ocasiones en que B mienta y A diga la verdad, luego la afirmación de A también será falsa.

La falsedad de la primera implica la falsedad de la segunda y al contrario. En definitiva, no puede ser que uno mienta y el otro no.

4. Choque de trenes

Dos trenes van por la misma vía en direcciones opuestas. Un tren va a 130 km/h y el otro a 170 km/h. A ambos los separa una distancia de 115 kilómetros. ¿A qué distancia estarán al minuto de chocar?

 

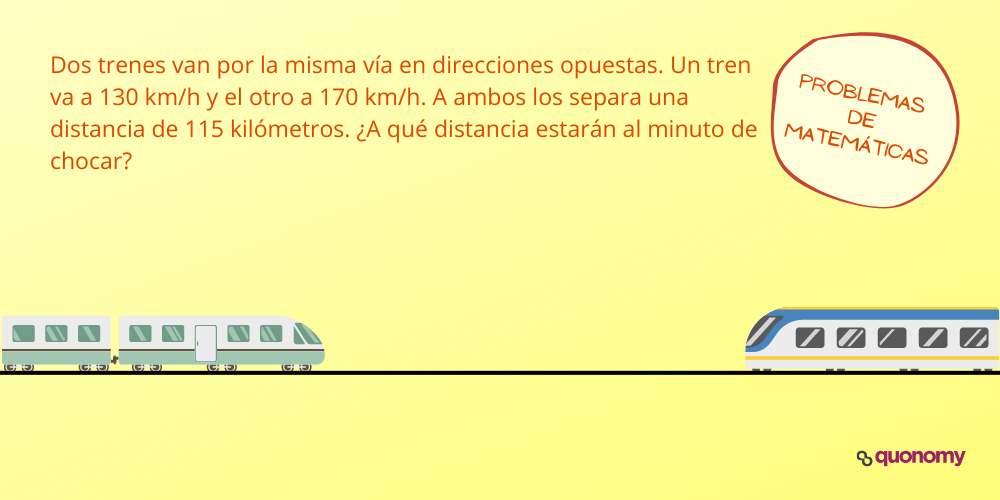
Solución: es un clásico problema de matemáticas con trenes. Si uno va a 130 km/h y otro a 170 km/h respectivamente, la velocidad relativa de acercamiento es de 300 km/h. Si pasamos a minutos este dato, tenemos que la velocidad es de 5k/minuto. Por lo tanto, un minuto antes de chocar estarán a 5 kilómetros.

5. Un problema de matemáticas difícil

Un agricultor tiene 300 manzanas y un caballo para transportarlas. El elefante puede cargar como máximo 100 manzanas y además, come una manzana por kilómetro. El mercado está a 100 kilómetros. ¿Cuántas manzanas podrá llevar, como máximo, el agricultor al mercado? Te damos una pista: el agricultor necesitará crear depósitos de manzanas en su viaje de ida y vuelta que le sirvan de aprovisionamiento.

 

Solución: el agricultor necesita crear depósitos de manzanas intermedios para que le sea rentable. Le servirán de aprovisionamiento ya que ha de hacer el viaje de ida y el de vuelta. Para llevar las 3000 manzanas iniciales a una distancia de x km el elefante consume 5x manzanas (dos viajes de ida y vuelta, puesto que su carga máxima es 1.000, y uno de ida).

A x km del punto de partida puede, pues, crear un depósito de 3.000-5x manzanas. Lo lógico es que deje un número entero de miles de manzanas en el el primer depósito para que el elefante empiece cada viaje con carga máxima.

De esta manera, 3.000-5x= 2.000, de donde x=200.

Para llevar 2.000 manzanas a ykm, el elefante consume 3y manzanas (un viaje de ida y vuelta y otro de ida), y a esa distancia le conviene dejar un depósito de 1.000.

De esta manera, 2.000 - 3y= 1.000, de donde y= 333.

Un último viaje del elefante hará llegar al mercado 1.000-(1.000-333-200)=533 plátanos.

6. Problema de matemáticas con rima

A un cerezo subí
donde cerezas había
y cerezas no cogí
y cerezas no dejé
¿Cuántas cerezas hallé?

 

Solución: este problema de matemáticas tiene ya unos cuantos años, ¿lo conoces? Había dos cerezas, cogiste una, dejaste otra. ¿Cómo? Subiste a un cerezo que tenía dos cerezas, no comiste "cerezas" en plural, sino sólo una "cereza", por lo que dejaste una en el árbol. 

7. El reloj

¿Cuántas veces, después de la medianoche y antes del mediodía, la aguja de los minutos coincide con la de las horas?

 

Solución: ¿has contestado 11? No te preocupes, la mayor parte de la gente comete este error. Sin embargo, solo coincide 10 veces. Toma un reloj de manecillas y compruébalo.

8. El mago

Tres amigas van a un espectáculo de magia cuya entrada cuesta 2 euros. Una de ellas le da 10 euros al taquillero, que además es el mago del espectáculo, y este, sin mediar palabra, le da 3 entradas y la vuelta. ¿Cómo supo el mago que las tres amigas iban juntas y que le había dado 10 euros para pagar lo de todas?

 

Solución: a priori no parece que el mago tenga datos suficientes para saber que iban juntas y que una iba a pagar lo de todas. Pero realmente a quien le falta un dato es a ti. Lo que ocurre es que quien paga lo hace con dos billetes de 5 euros, por lo tanto, es evidente que quiere 3 entradas. De querer una o dos, solo habría dado un billete. 

9. Un problema matemático clásico

Un aviador le dice a un amigo: 

- Mañana vuelo a Madrid, le dice un aviador a un amigo.

- Si no tuvieras que desviarte mucho de tu rumbo, ¿podrías llevarle un paquete a mi hermana?, comenta el amigo.

- Por supuesto, puedo hacerlo sim problema, dice el aviador sin que el amigo le diga dónde vive su hermana. No tendré que desviarme.

¿Dónde tiene lugar esta conversación?

Pista: ten en mente qué forma tiene la Tierra.

 

Solución: la conversación tiene lugar en Nueva Zelanda, que está en las antípodas de España. De esta manera, al aviador le da igual recorrer cualquier semicírculo de la esfera terrestre. Puede pasar por cualquier lugar de la Tierra para llegar a Madrid.

10. Operaciones matemáticas

Tienes que una cazuela en el fuego que ha de hervir durante 15 minutos. Solo dispones de dos relojes de arena, uno de 11 minutos y otro de 7. ¿Cómo puedes hacer para medir con ellos un cuarto de hora exacto?

 

Solución: comienzas poniendo en marcha los dos relojes al mismo tiempo. Cuando el de los 7 minutos se agote, le das la vuelta. Como en el de 11 minutos quedan aun 4 minutos, en el de 7 habrán pasado 4, por lo que habrás de dar de nuevo la vuelta al de 7 minutos cuando se agote el de 11. De esta manera tendrás 11 + 4=15.